Ellipse

Ellipse can be defined in several ways. One of them is to say that an ellipse represents the locus of all points whose sum of distances from two fixed points - foci - is a constant. Here is the derivation of the equation of an ellipse in polar coordinates. If we place the origin of the coordinate system at one of the foci, denote the sum of distances with $l$, the distance between the two foci with $2f$, and use the cosine theorem, we have:

\[\begin{align*} &\sqrt{r^{2}+4f^{2}-4rf\cos{\theta}} + r = l \\ &r^{2}+4f^{2}-4rf\cos{\theta} = l^{2} + r^{2} - 2lr \\ &2r(l-2f\cos{\theta}) = l^{2}-4f^{2} \end{align*}\]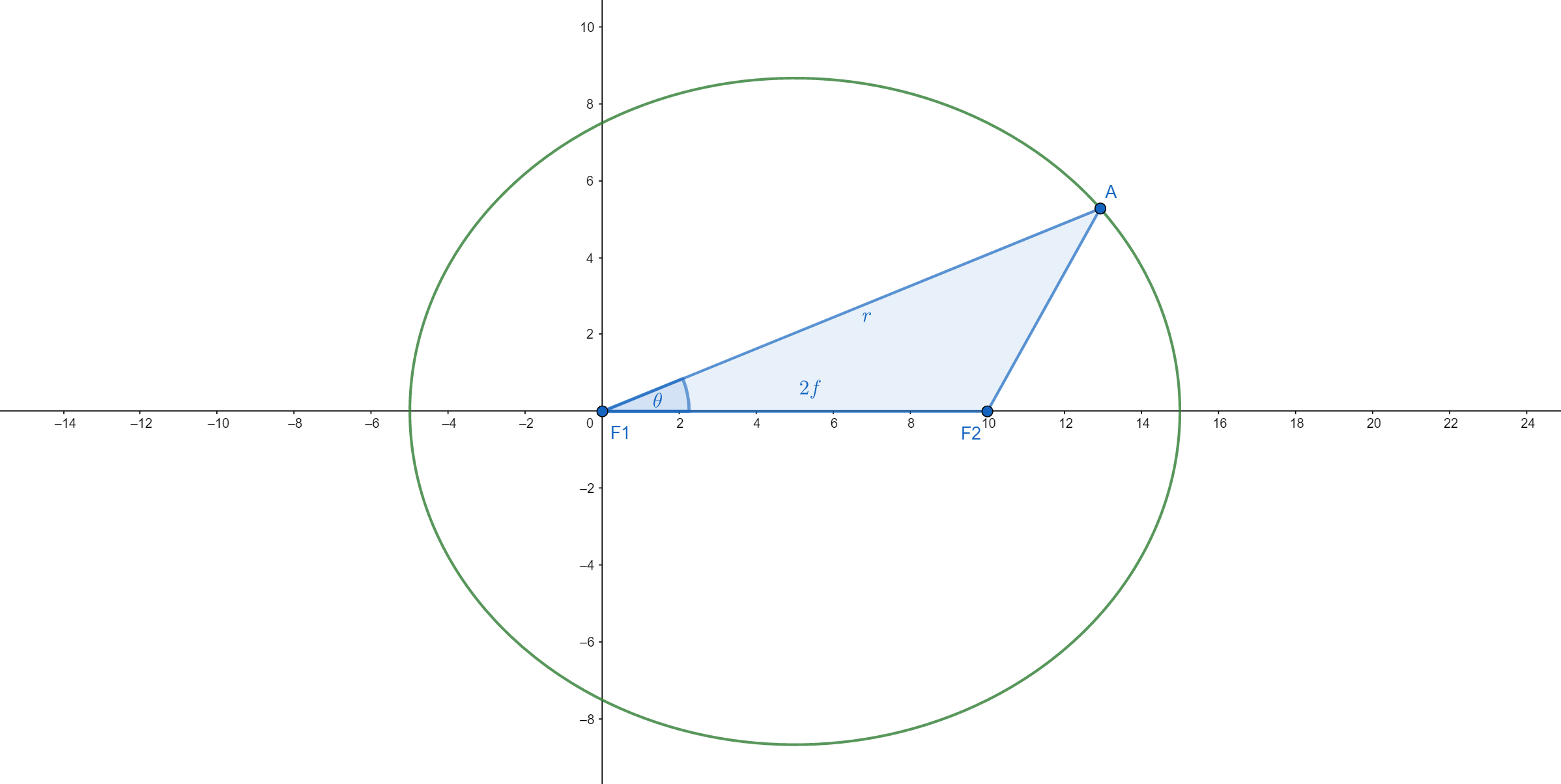

If the length of the major axis is equal to $2a$, then we have $l=2a$, and if we introduce the ratio $e=f/a$ as the eccentricity of the ellipse, we get:

\[\begin{align*} &4ar(1-e\cos{\theta})=4a^{2}(1-e^{2}) \\ &r = a\dfrac{1-e^{2}}{1-e\cos{\theta}} \end{align*}\]

If we consider the reciprocal value $\rho = 1/r$ and seek its derivative with respect to $\theta$, we get:

\[\begin{align*}\rho &= \frac{1-e\cos{\theta}}{a(1-e^{2})} \\ \frac{d\rho}{d\theta} &= \frac{e\sin{\theta}}{a(1-e^{2})} \\ \left(\frac{d\rho}{d\theta}\right)^{2}+\rho^{2} &= \frac{1-2e\cos\theta+e^{2}}{a^{2}(1-e^{2})^{2}} \\ \left(\frac{d\rho}{d\theta}\right)^{2}+\rho^{2} &= 2\frac{1-e\cos\theta}{a^{2}(1-e^{2})^{2}} + \frac{e^{2}-1}{a^{2}(1-e^{2})^{2}} \\ \left(\frac{d\rho}{d\theta}\right)^{2}+\rho^{2} &= \frac{1}{a(1-e^{2})}\left(2\rho-\frac{1}{a}\right)\end{align*}\]

These equations can be further simplified if we introduce the constant $1/C = a(1-e^{2})$:

\[\begin{align*} \left(\frac{d\rho}{d\theta}\right)^{2}+\rho^{2} &= C\left(2\rho-\frac{1}{a}\right) \\ \left(\frac{d\rho}{d\theta}\right)^{2}+ (\rho - C)^{2} &= C\left(C-\frac{1}{a}\right)\end{align*}\]